A simple benchmark of various math operations

How computationally expensive are various fundamental floating point mathematical operations?  Here’s a quick and dirty benchmark, which, although surely quite naive, seems to capture the rough relative cost of a few operations.

Motivation

This quarter I am taking a course on numerical linear algebra.  Naturally, we are covering topics like the fundamentals of floating point arithmetic, numerical stability, matrix decompositions, and algorithm analysis.

In a few of our assignments, we are tasked with determining the exact number of floating point operations (FLOPs) required to execute some particular algorithm. Analyzing the complexity of algorithms is certainly a useful exercise, but it’s silly to give the impression that we can produce the exact FLOP count.  I’m not much of a hardware guy, but I at least know that modern CPUs are stupendously complex, and any FLOP count we can write down on paper after inspecting pseudocode has no chance at being “exact” in any meaningful way.

Besides the overall futility of these exercises, we are instructed to consider each of the following operations as a baseline of “1 FLOP”: addition, subtraction, multiplication, division, square root.  As we will see shortly, these operations are not even close to equivalent in terms of real-world computational expense, so it’s misleading to count these all as equal atoms of computation.

Anyways… on one recent assignment we were asked to look at the FLOP count for some technique that used a rotation matrix.  As you might expect for rotation-y stuff, the matrix entries were based on various trigonometric functions (sine, cosine, arctan).  I was in a rush when doing the assignment, so I casually assigned 1 FLOP to each of these trig functions.  I felt partially justified in doing this, as I had just learned that these trig functions are in fact offered as single CPU instructions in modern Intel x86.  Given that we were glossing over so much already, it seemed excusable to consider as atomic anything that can theoretically be done in a single CPU instruction. Regardless, I was docked points. Hmph.

OK fine, I’m not worried about the points, but now I’m curious about how expensive these operations really are.  If “square root” qualifies as 1 FLOP, is it really so wrong to lump in “sine” as 1 FLOP, too?

Benchmark

I dusted off the C++ region of my brain, and hacked up the following test program. It was fun to (ab)use macros heavily here.

#include <math.h>
#include <chrono>
using namespace std;
using namespace std::chrono;

// timer cribbed from
// https://gist.github.com/gongzhitaao/7062087
class Timer
{
public:
    Timer() : beg_(clock_::now()) {}
    void reset() { beg_ = clock_::now(); }
    double elapsed() const {
        return duration_cast<second_>
            (clock_::now() - beg_).count();
    }

private:
    typedef high_resolution_clock clock_;
    typedef duration<double, ratio<1>> second_;
    time_point<clock_> beg_;
};

int main(char* argv)
{
    double total;
    Timer tmr;

#define randf() ((double) rand()) / ((double) (RAND_MAX))
#define OP_TEST(name, expr)               \
    total = 0.0;                          \
    srand(42);                            \
    tmr.reset();                          \
    for (int i = 0; i < 100000000; i++) { \
        double r1 = randf();              \
        double r2 = randf();              \
        total += expr;                    \
    }                                     \
    double name = tmr.elapsed();          \
    printf(#name);                        \
    printf(" %.7f\n", name - baseline);

    // time the baseline code:
    //   for loop with no extra math op
    OP_TEST(baseline, 1.0)

    // time various floating point operations.
    //   subtracts off the baseline time to give
    //   a better approximation of the cost
    //   for just the specified operation
    OP_TEST(plus, r1 + r2)
    OP_TEST(minus, r1 - r2)
    OP_TEST(mult, r1 * r2)
    OP_TEST(div, r1 / r2)
    OP_TEST(sqrt, sqrt(r1))
    OP_TEST(sin, sin(r1))
    OP_TEST(cos, cos(r1))
    OP_TEST(tan, tan(r1))
    OP_TEST(atan, atan(r1))
    OP_TEST(exp, exp(r1))
}

Results

Compiling this benchmark non-optimized (so that nothing gets erased or rearranged) and running on my Intel Core i7 machine, I get the following results.  I’ve normalized so results are relative to the cost of “plus.”

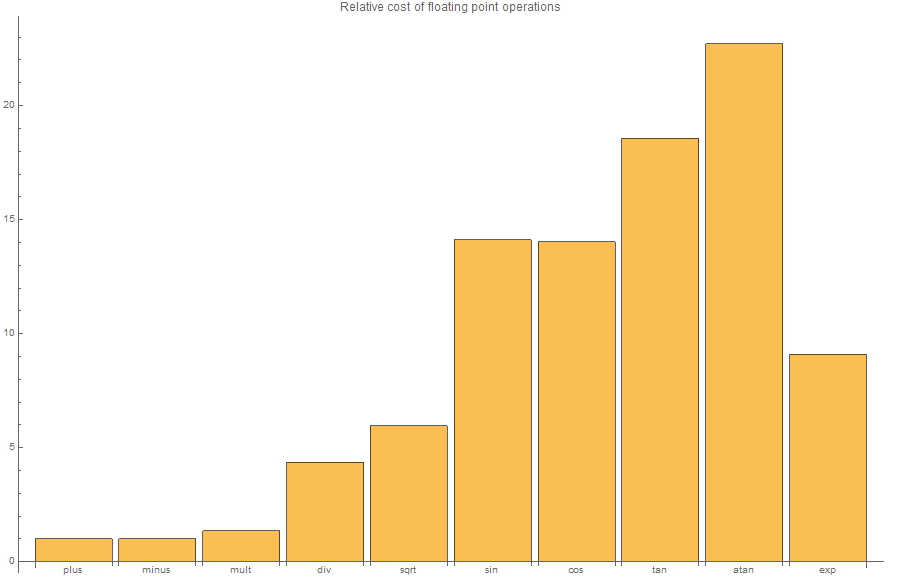
So of the “1 FLOP” operations, it turns out division and square root are really about 4x and 6x as expensive, respectively, as the baseline of addition. Trig functions appear to land somewhere in the 15x-20x range, and exp about 10x.

So yes, trig functions really are significantly more expensive than +-*√ (though it still seems a bit arbitrary to count sqrt and division as 1 FLOP).