How many coffee sleeves make a circle?

When you get a coffee or tea in a paper cup, often you will get one of those cardboard sleeves along with it that helps keep the grippable surface of the cup at a reasonable temperature.  When those sleeves are on the cup, their top and bottom appear flat, parallel to the top and bottom of the cup.  When you take the sleeve off and flatten it, however, you notice that the top and bottom actually have a slight curve to them, and that the flat sleeve is in the shape of a small arc.

This would indicate that placing a bunch of flattened sleeves end-to-end with their edges flush would eventually result in a big circle (assuming the sleeve-arc has uniform width).  How many sleeves would that take, and how big would the circle be?

Here’s a typical sleeve used with the coffee cups from my work.  Let’s define \(r_1\) and \(r_2\) as the straight-line measurement across the top and bottom of the sleeve, respectively,  and \(h\) as the measurement flush along the edge of the sleeve.

To figure out how many sleeves we need to complete a circle, we need to know what angle the sleeve subtends.  Let’s call that angle \(\Phi\) . Here’s a slightly exaggerated diagram that makes it clear exactly how the dimensions relate.

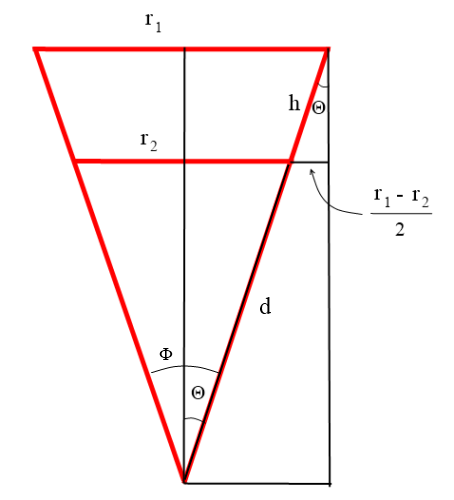
The angle we are interested in is \(\Phi = 2\Theta\) .  From the diagram we can see that \(\sin(\Theta) = \frac{r_1 - r_2}{2h}\) , and therefore  \(\Phi=2 \Theta=2\sin^{-1}(\frac{r_1 - r_2}{2h})\) .  The number of sleeves needed to create a full circle will be \(2\pi/\Phi\) .

How big is this circle?  We don’t even need to use trig for that part.  Properties of similar triangles tell us that \(\frac{r_1}{d+h} = \frac{r_2}{d}\) and therefore the inner radius \(d = \frac{h r_2}{r_1 - r_2}\) and outer radius \(d + h = \frac{h r_1}{r_1 - r_2}\) .

Directly measuring my coffee sleeve, I observe that \(r_1 = 4.94^{\prime \prime}\) , \(r_2 = 4.25^{\prime \prime}\) , and \(h = 2.31^{\prime \prime}\) .  Plugging these in, we find that \(\Phi \approx 17.2^{\circ}\) , indicating we need just under 21 sleeves to form a full circle.  That circle will have inner radius 14.2” and outer radius 16.5”.

Lo and behold, it works: