Expected return on a Mega Millions ticket

The recent record-breaking Mega Millions lottery drawing got me wondering how much a lotto ticket is really worth.  What are the odds of winning, and based on those odds and the size of the jackpot, what are the expected winnings from a Mega Millions ticket?

The Mega Millions website breaks down the odds, and the different ways you can win.  Let’s look at how those odds play out.

Odds of winning

Each ticket consists of 5 numbers from the range 1 to 56 (inclusive), and 1 “mega” number from the range 1 to 46 (inclusive).  Repeats are not allowed, and order does not matter.  There are \(56 \choose 5\) = 3,819,816 ways to pick the 5 regular numbers, and \(46 \choose 1\) = 46 ways to pick the mega number.  Therefore the total number of possible tickets is \({56 \choose 5} {46 \choose 1}\) = 3,819,816 * 46 = 175,711,536.

Jackpot/5 numbers correct

The odds of hitting the jackpot are pretty easy to compute.  There is 1 way to pick the 5 regular numbers correctly out of 3,819,816 possibilities, and 1 way to pick the mega number correctly out of 46 possibilities.  Therefore the probability of doing both is \(P_{5,1} =\) ¹⁄_3819816 * ¹⁄₄₆ = ¹⁄_175711536.

Following the same logic, we can find the odds of picking the 5 regular numbers correctly, but missing the mega number.  There is 1 way to do the former, but 45 ways to do the latter, so we come to a probability \(P_{5,0} =\)  1/3819816 * ⁴⁵⁄₄₆ = 46 / 175711536 = 5/19523504 ~ ¹⁄_3904701.

There is always a ¹⁄₄₆ chance of hitting the mega number, and a ⁴⁵⁄₄₆ chance of missing it.  The tricky part is determining the odds of hitting some subset of the 5 regular numbers.

4 numbers correct

What are the chances of hitting exactly 4 out of 5 regular numbers?  Let’s fix the 4 numbers we got right.  There are 56 - 4 = 52 options for our 5th number.  But 1 of those 52 is the correct 5th number, which we aren’t allowed to pick, since we are asserting that we got exactly 4 right.  Thus we have 51 options for our 5th number.  Additionally, we need to take into account the fact that there is more than 1 way to get 4 out of 5 right.  There are \(5 \choose 4\) ways, and each of those presents 51 choices for the 5th number.

So we come to final probability of \(P_{4,1}=51 {5 \choose 4} / {56 \choose 5} \times \frac{1}{46} \) = 85/58570512 ~ ¹⁄₆₈₉₀₆₅ (with mega number) and \(P_{4,0}=51 {5 \choose 4} / {56 \choose 5} \times \frac{45}{46}\) = 1275/19523504 ~ 1/15313 (no mega number).

3 numbers correct

Hitting exactly 3 out of 5 is even a bit trickier.  Fix the 3 we got right, leaving 56 - 3 = 53 options for the final 2 numbers.  But we can’t pick _either_ of the 2 remaining correct numbers, so really there are only 53 - 2 = 51 options (see a pattern?).  Since we are picking 2 numbers from a pool of 51 options, we have \(51 \choose 2\) ways to pick.  Finally, we also realize there are \(5 \choose 3\) ways to get 3 out of 5 right.

Thus our final probability is \(P_{3,1}={51 \choose 2} {5 \choose 3} / {56 \choose 5} \times \frac{1}{46} \) = 2,¹²⁵⁄₂₉,285,256 ~ ¹⁄₁₃,781 (with mega number) and \(P_{3,0}={51 \choose 2} {5 \choose 3} / {56 \choose 5} \times \frac{45}{46} \)  = 31875/9761752 ~ ¹⁄₃₀₆ (no mega number).

In general

We can see the general formula now.  The odds of hitting exactly \(n\) numbers are

and

Splitting the jackpot

If we were the only one playing the lotto, we would be pretty much done.  We know the odds of winning each prize, and we know the value of the prizes, so we could do a quick calculation to compute our expected winnings.   There is one more thing to consider, though - the odds of splitting the jackpot.

The rules state that in the event of multiple jackpot winners, the jackpot will be split evenly between them (smaller prizes are not split).  With a small pool of players, one would not expect very many jackpot winners.  But with a huge number of players, it becomes increasingly likely that the jackpot will be split.

So what we need to figure out is - in the event that we hit the jackpot, what is the expected value of that jackpot after splitting?

In the event that we hit the jackpot, how many other people do we expect to have also won?  Well, that’s actually the same as the total number of people we expect to win, without any additional knowledge, and assuming a large pool of players.  In other words, the fact that we’ve won does not change anyone else’s odds of winning.

Let’s call the total number of players \(K\) and the total jackpot size \(J\) .  We know the probability of hitting the jackpot is \(P_{5,1}\) .  Then the expected number of winners (without knowing our own result) \(\lambda\) is defined by \(\lambda=P_{5,1}K\) .

The exact number of winners follows an approximate Poisson distribution, so the probability of exactly \(k\) winners is \(\frac{\lambda^k e^{- \lambda}}{k!} \) .  As argued above, this is the same probability of \(k\) other people winning, given that we have won.

So, in the event that we have won, our expectation for the effective jackpot \(J^{\prime}\) is

$$ J^{\prime}=\sum_{k=0}^{K}\frac{J}{k+1}\frac{\lambda^k e^{- \lambda}}{k!}$$

Where the last step is taking advantage of the fact that   \(\sum_{k=0}^{K}\frac{\lambda^k e^{- \lambda}}{k!} = 1\) because this represents the sum of probabilities of all possible outcomes.

So we see that the expected effective jackpot is a bit smaller than the total jackpot divided by the expected number of winners.

Putting it all together

Ok, so what’s our final result?  Given a jackpot size \(J\) and number of players \(K\) , the expected number of jackpot winners is \(\lambda=P_{5,1}K\) , and the expected winnings \(E(W)\) from a single ticket will be:

\(E(W) = \) \( P_{5,1} \times \frac{J}{\lambda}(1-e^{-\lambda}) +\) \( P_{5,0} \times 250,000 +\) \( P_{4,1} \times 10,000 +\) \( P_{4,0} \times 150 +\) \( P_{3,1} \times 150 +\) \( P_{3,0} \times 7 +\) \( P_{2,1} \times 10 +\) \( P_{1,1} \times 3 +\) \( P_{0,1} \times 2\)

The recent record-breaking Mega Millions had a jackpot of $650 million.  I don’t know exactly how many tickets were sold, but I read an article that estimated it could be as many as 300 million.  Using those numbers, the expected winnings come out to $1.96.

So yes, as far as I can tell, playing this particular Mega Millions was actually a double-your-money proposition, statistically speaking.  That isn’t true in general, though.  Reducing the jackpot and number of players to more typical levels (say $100 million jackpot, with 50 million players) brings the expectation down to $0.68, clearly a bad bet.

Plotting expected winnings vs jackpot size vs number of players, we get the following plot (jackpot from $1 to $1B, players from 100 to 350M):

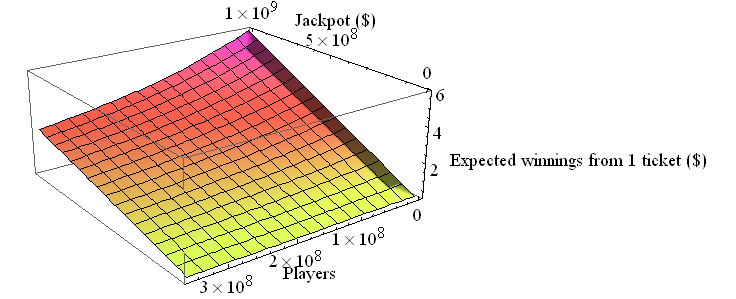
Fixing the number of players at 100M, buying a ticket becomes an even-money bet when the jackpot climbs to around $190M.  Of course, with larger jackpots more people will be playing, which reduces expected winnings, so really the threshold is somewhat higher.  Plus there are also taxes to consider, and the fact that the lump sum prize is always smaller than the annuities prize.

I think my takeaway from the whole thing is that it’s more interesting to study the lottery than to actually play it (I am embarrassed to admit mathematically proud to announce that I played 10 tickets on this lottery, and won $0).

[Credit to this site for guidance on working through the jackpot-splitting stuff.]